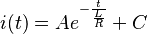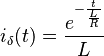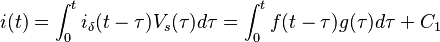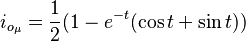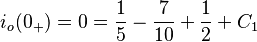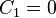Impulsantwort

Bisher wurden die Stromkreise von einer Gleichstromquelle, einer Wechselstromquelle und einer exponentiellen Quelle betrieben. Wenn wir den Strom einer Schaltung finden können, die von einer Dirac-Deltafunktion oder einer Stoßspannungsquelle δ erzeugt wird, dann kann das Convolution Integral verwendet werden, um den Strom zu einer bestimmten Spannungsquelle zu finden!

Beispiel Impulsantwort

Der Strom wird durch die Ableitung des durch eine Gleichspannungsquelle gefundenen Stroms ermittelt! Angenommen, das Ziel ist es, den δ-Strom einer LR-Schaltung der Serie zu finden, so dass in Zukunft das Convolution Integral verwendet werden kann, um den Strom einer beliebigen Quelle zu finden.

Wählen Sie eine DC-Quelle von 1 Volt (das reale Vs kann dann davon abweichen). Die besondere homogene Lösung (stationärer Zustand) ist 0, die homogene Lösung zur inhomogenen Gleichung hat die Form:

$i(t) = Ae^{-\frac{t}{\frac{L}{R}}} + C$

Angenommen, der Strom im Induktor ist zunächst Null. Die Anfangsspannung wird 1 sein und über dem Induktor liegen (da kein Strom fließt):

$v(t) = L{d i(t) \over dt}$:$v(0) = 1 = L * (-\frac{A R}{L})$:$A = -1/R$

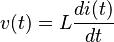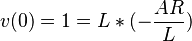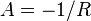
Wenn der Strom im Induktor zunächst Null ist, dann:

$i(0) = 0 = A + C$

Das impliziert:

$C = -A = 1/R$

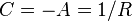
Die Antwort auf das Einschalten einer Gleichspannungsquelle bei t=0 bis ein Volt (die so genannte Unit Response μ) lautet also:

$i_\mu (t) = \frac{1}{R}(1 - e^{-\frac{t}{\frac{L}{R}}})$

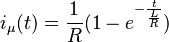
Wenn man die Ableitung daraus zieht, erhält man den Impuls (δ) Strom ist:

$i_\delta (t) = \frac{e^{-\frac{t}{\frac{L}{R}}}}{L}$

Nun der Strom aufgrund einer beliebigen Anzahl V_S(t) kann über das Convolution Integral gefunden werden:

$i(t) = \int_0^t i_\delta (t-\tau) V_s(\tau) d\tau = \int_0^t f(t-\tau)g(\tau)d\tau + C_1$

Sie sollten i_δ nicht als aktuell betrachten. Es ist wirklich 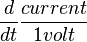${d \over dt}\frac{current}{1 volt}$. V_S(τ) wird zu einem Multiplikator.

LRC Beispiel

Finden Sie den Zeitbereichsausdruck für i_o, da I_s = cos(t + π/2)μ(t) amp.

Früher wurde die Step-Response für dieses Problem gefunden:

$i_{o_\mu} = \frac{1}{2}(1 - e^{-t}(\cos t + \sin t))$

Die Impulsantwort wird die Ableitung davon sein:

$i_{o_\delta} = {d i_{o_\mu} \over dt} = 0 + \frac{1}{2}e^{-t}(\cos t + \sin t) - \frac{1}{2}e^{-t}(-\sin t + \cos t)$

$i_{o_\delta} = \frac{1}{2}e^{-t}(\cos t + \sin t + \sin t - \cos t) = e^{-t}\sin t$:$I_s = 1 + \cos t$

$i_o(t) = \int_0^t i_{o_\delta} (t-\tau) I_s(\tau) d\tau + C_1$

$i_o(t) = \int_0^t e^{-(t-\tau)}\sin (t-\tau) (1 + \cos \tau) d\tau + C_1$

$i_o(t) = \frac{\cos t}{5} + \frac{2 \sin t}{5} - \frac{7 e^{-t}\cos t}{10} - \frac{11 e^{-t}\sin t}{10} + \frac{1}{2} + C_1$

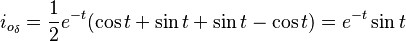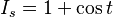
Der Mupad-Code zur Lösung des Integrals (ersetzt x durch τ) ist:

f := exp(-(t-x)) *sin(t-x) *(1 + cos(x));<br>S := int(f,x = 0..t)

Auffinden der Integrationskonstante

$i_o(0_+) = 0 = \frac{1}{5} - \frac{7}{10} + \frac{1}{2} + C_1$

Das impliziert:

$C_1 = 0$