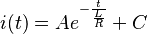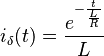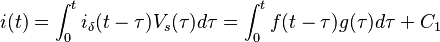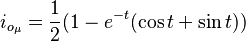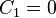Impulsantwort: Unterschied zwischen den Versionen
Rheigl (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Bisher wurden die Stromkreise von einer Gleichstromquelle, einer Wechselstromquelle und einer exponentiellen Quelle betrieben. Wenn wir den Strom einer Schaltu…“) |
(Kleinere Tippfehler ausgebessert) |
Bisher wurden die Stromkreise von einer Gleichstromquelle, einer Wechselstromquelle und einer exponentiellen Quelle betrieben. Wenn wir den Strom einer Schaltung finden können, die von einer Dirac-Deltafunktion oder einer Stoßspannungsquelle δ erzeugt wird, dann kann das Convolution Integral verwendet werden, um den Strom zu einer bestimmten Spannungsquelle zu finden!
Beispiel Impulsantwort[Bearbeiten | Quelltext bearbeiten]
Der Strom wird durch die Ableitung des durch eine Gleichspannungsquelle gefundenen Stroms ermittelt! Angenommen, das Ziel ist es, den δ-Strom einer LR-Schaltung der Serie zu finden ... , so dass in Zukunft das Convolution Integral verwendet werden kann, um den Strom einer beliebigen Quelle zu finden. ..!
Wählen Sie eine DC-Quelle von 1 Volt (das reale Vs kann dann davon abweichen). Die besondere homogene Lösung (stationärer Zustand) ist 0, die homogene Lösung zur inhomogenen Gleichung hat die Form:
Angenommen, der Strom im Induktor ist zunächst Null. Die Anfangsspannung wird 1 sein und über dem Induktor liegen (da kein Strom fließt):
-
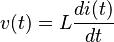 :
: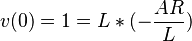 :
: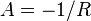
Wenn der Strom im Induktor zunächst Null ist, dann:
-
 Which implies that
Which implies that
- Das impliziert:
-
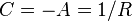
- Die Antwort auf das Einschalten einer Gleichspannungsquelle bei t=0 bis ein Volt (die so genannte Unit Response μ) lautet also:
-
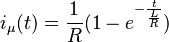
Wenn man die Ableitung daraus zieht, erhält man den Impuls (δ) Strom ist:
Nun der Strom aufgrund einer beliebigen Anzahl VS(t) kann über das Convolution Integral gefunden werden:
Sie sollten iδ nicht als aktuell betrachten. Es ist wirklich 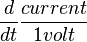 . VS(τ) wird zu einem Multiplikator.
. VS(τ) wird zu einem Multiplikator.
LRC NeispielBeispiel[Bearbeiten | Quelltext bearbeiten]
Finden Sie den Zeitbereichsausdruck für io, da Is = cos(t + π/2)μ(t) amp.
Früher wurde die Step-Response für dieses Problem gefunden:
Die Impulsantwort wird die Ableitung davon sein:
-

-
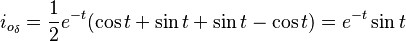 :
: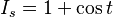
-

-

-

f := exp(-(t-x)) *sin(t-x) *(1 + cos(x));<br>S := int(f,x = 0..t)
Auffinden der Integrationskonstante[Bearbeiten | Quelltext bearbeiten]
Das impliziert:
Bisher wurden die Stromkreise von einer Gleichstromquelle, einer Wechselstromquelle und einer exponentiellen Quelle betrieben. Wenn wir den Strom einer Schaltung finden können, die von einer Dirac-Deltafunktion oder einer Stoßspannungsquelle δ erzeugt wird, dann kann das Convolution Integral verwendet werden, um den Strom zu einer bestimmten Spannungsquelle zu finden!
==Beispiel Impulsantwort==
Der Strom wird durch die Ableitung des durch eine Gleichspannungsquelle gefundenen Stroms ermittelt! Angenommen, das Ziel ist es, den δ-Strom einer LR-Schaltung der Serie zu finden ... , so dass in Zukunft das Convolution Integral verwendet werden kann, um den Strom einer beliebigen Quelle zu finden...!
Wählen Sie eine DC-Quelle von 1 Volt (das reale Vs kann dann davon abweichen). Die besondere homogene Lösung (stationärer Zustand) ist 0, die homogene Lösung zur inhomogenen Gleichung hat die Form:
:<math>i(t) = Ae^{-\frac{t}{\frac{L}{R}}} + C </math>
Angenommen, der Strom im Induktor ist zunächst Null. Die Anfangsspannung wird 1 sein und über dem Induktor liegen (da kein Strom fließt):
:<math>v(t) = L{d i(t) \over dt}</math>:<math>v(0) = 1 = L * (-\frac{A R}{L})</math>:<math>A = -1/R</math>
Wenn der Strom im Induktor zunächst Null ist, dann:
:<math>i(0) = 0 = A + C</math>Which implies that:
:
:Das impliziert:
:<math>C = -A = 1/R</math>
:Die Antwort auf das Einschalten einer Gleichspannungsquelle bei t=0 bis ein Volt (die so genannte Unit Response μ) lautet also:
:<math>i_\mu (t) = \frac{1}{R}(1 - e^{-\frac{t}{\frac{L}{R}}})</math>
Wenn man die Ableitung daraus zieht, erhält man den Impuls (δ) Strom ist:
:<math>i_\delta (t) = \frac{e^{-\frac{t}{\frac{L}{R}}}}{L}</math>
Nun der Strom aufgrund einer beliebigen Anzahl V<sub>S</sub>(t) kann über das Convolution Integral gefunden werden:
:<math>i(t) = \int_0^t i_\delta (t-\tau) V_s(\tau) d\tau = \int_0^t f(t-\tau)g(\tau)d\tau + C_1</math>
Sie sollten i<sub>δ</sub> nicht als aktuell betrachten. Es ist wirklich <math>{d \over dt}\frac{current}{1 volt}</math>. V<sub>S</sub>(τ) wird zu einem Multiplikator.
==LRC NeispielBeispiel==
Finden Sie den Zeitbereichsausdruck für i<sub>o</sub>, da I<sub>s</sub> = cos(t + π/2)μ(t) amp.
Früher wurde die Step-Response für dieses Problem gefunden:
:<math> i_{o_\mu} = \frac{1}{2}(1 - e^{-t}(\cos t + \sin t))</math>
Die Impulsantwort wird die Ableitung davon sein:
:<math>i_{o_\delta} = {d i_{o_\mu} \over dt} = 0 + \frac{1}{2}e^{-t}(\cos t + \sin t) - \frac{1}{2}e^{-t}(-\sin t + \cos t)</math>
:<math>i_{o_\delta} = \frac{1}{2}e^{-t}(\cos t + \sin t + \sin t - \cos t) = e^{-t}\sin t</math>:<math>I_s = 1 + \cos t</math>
:<math>i_o(t) = \int_0^t i_{o_\delta} (t-\tau) I_s(\tau) d\tau + C_1</math>
:<math>i_o(t) = \int_0^t e^{-(t-\tau)}\sin (t-\tau) (1 + \cos \tau) d\tau + C_1</math>
:<math>i_o(t) = \frac{\cos t}{5} + \frac{2 \sin t}{5} - \frac{7 e^{-t}\cos t}{10} - \frac{11 e^{-t}\sin t}{10} + \frac{1}{2} + C_1</math>
Der Mupad-Code zur Lösung des Integrals (ersetzt x durch τ) ist:<pre>f := exp(-(t-x)) *sin(t-x) *(1 + cos(x));<br>S := int(f,x = 0..t)</pre>
==Auffinden der Integrationskonstante==
:<math>i_o(0_+) = 0 = \frac{1}{5} - \frac{7}{10} + \frac{1}{2} + C_1</math>
Das impliziert:
:<math>C_1 = 0</math>| Zeile 1: | Zeile 1: | ||
Bisher wurden die Stromkreise von einer Gleichstromquelle, einer Wechselstromquelle und einer exponentiellen Quelle betrieben. Wenn wir den Strom einer Schaltung finden können, die von einer Dirac-Deltafunktion oder einer Stoßspannungsquelle δ erzeugt wird, dann kann das Convolution Integral verwendet werden, um den Strom zu einer bestimmten Spannungsquelle zu finden! | Bisher wurden die Stromkreise von einer Gleichstromquelle, einer Wechselstromquelle und einer exponentiellen Quelle betrieben. Wenn wir den Strom einer Schaltung finden können, die von einer Dirac-Deltafunktion oder einer Stoßspannungsquelle δ erzeugt wird, dann kann das Convolution Integral verwendet werden, um den Strom zu einer bestimmten Spannungsquelle zu finden! | ||
==Beispiel Impulsantwort== | ==Beispiel Impulsantwort== | ||
| − | Der Strom wird durch die Ableitung des durch eine Gleichspannungsquelle gefundenen Stroms ermittelt! Angenommen, das Ziel ist es, den δ-Strom einer LR-Schaltung der Serie zu finden | + | Der Strom wird durch die Ableitung des durch eine Gleichspannungsquelle gefundenen Stroms ermittelt! Angenommen, das Ziel ist es, den δ-Strom einer LR-Schaltung der Serie zu finden, so dass in Zukunft das Convolution Integral verwendet werden kann, um den Strom einer beliebigen Quelle zu finden. |
Wählen Sie eine DC-Quelle von 1 Volt (das reale Vs kann dann davon abweichen). Die besondere homogene Lösung (stationärer Zustand) ist 0, die homogene Lösung zur inhomogenen Gleichung hat die Form: | Wählen Sie eine DC-Quelle von 1 Volt (das reale Vs kann dann davon abweichen). Die besondere homogene Lösung (stationärer Zustand) ist 0, die homogene Lösung zur inhomogenen Gleichung hat die Form: | ||
| Zeile 13: | Zeile 13: | ||
Wenn der Strom im Induktor zunächst Null ist, dann: | Wenn der Strom im Induktor zunächst Null ist, dann: | ||
| − | :<math>i(0) = 0 = A + C</math> | + | :<math>i(0) = 0 = A + C</math> |
| − | :<math>C = -A = 1/R</math>Die Antwort auf das Einschalten einer Gleichspannungsquelle bei t=0 bis ein Volt (die so genannte Unit Response μ) lautet also: | + | :Das impliziert: |
| + | :<math>C = -A = 1/R</math> | ||
| + | :Die Antwort auf das Einschalten einer Gleichspannungsquelle bei t=0 bis ein Volt (die so genannte Unit Response μ) lautet also: | ||
:<math>i_\mu (t) = \frac{1}{R}(1 - e^{-\frac{t}{\frac{L}{R}}})</math> | :<math>i_\mu (t) = \frac{1}{R}(1 - e^{-\frac{t}{\frac{L}{R}}})</math> | ||
| Zeile 26: | Zeile 28: | ||
Sie sollten i<sub>δ</sub> nicht als aktuell betrachten. Es ist wirklich <math>{d \over dt}\frac{current}{1 volt}</math>. V<sub>S</sub>(τ) wird zu einem Multiplikator. | Sie sollten i<sub>δ</sub> nicht als aktuell betrachten. Es ist wirklich <math>{d \over dt}\frac{current}{1 volt}</math>. V<sub>S</sub>(τ) wird zu einem Multiplikator. | ||
| − | ==LRC | + | ==LRC Beispiel== |
Finden Sie den Zeitbereichsausdruck für i<sub>o</sub>, da I<sub>s</sub> = cos(t + π/2)μ(t) amp. | Finden Sie den Zeitbereichsausdruck für i<sub>o</sub>, da I<sub>s</sub> = cos(t + π/2)μ(t) amp. | ||